Guía No 2. Tercer Periodo. Octavo y Noveno. Áreas y Perímetros
IDENTIFICACIÓN
DE LA GUÍA DE APRENDIZAJE
Área: Matemáticas Tercer Periodo
|
Semana: Del 21 al 24 de Agosto
|
Grado: Octavo y noveno
|
|
Objetivo General: Aplicar los conceptos de perímetro y
área para resolver problemas de la
vida real.
|
|
Actividad a Realizar por el estudiante:
1.
Recordar cómo
calcular perímetro y área.
2.
Leer las
explicaciones acerca del teorema de Pitágoras y sus aplicaciones
3.
Mirar vídeos
para aclarar dudas.
4.
Resolver
problemas aplicando perímetro y áreas.
|
|
Criterios de Evaluación: La calidad de los procesos,
coherencia, orden y la entrega oportuna. Los trabajos se entregarán vía
correo electrónico o evidencia al whatsApp de cada docente, antes del viernes
24 de Agosto.
|
|
ESTRUCTURA DE LAS ACTIVIDADES DE APRENDIZAJE
2.
CONOCIMIENTOS NECESARIOS PARA EL APRENDIZAJE:
·
El perímetro de una figura es la medida
del contorno y el área es la medida de la superficie, la parte interna (se
desarrolló en una guía anterior)
·
Un triángulo rectángulo es el que tiene
un ángulo recto (90°). Ese ángulo, se sim-
boliza en el gráfico con un cuadrado. El la-
do que queda frente al ángulo recto se llama hipotenusa,
es el más largo, y los otros se llaman catetos.
|
|
·
TEOREMA DE
PITÁGORAS: En todo trián-
gulo rectángulo ABC, se cumple que el cuadrado
que se forma sobre la hipotenusa tiene la misma área que los dos cuadrados
que se forman sobre los dos catetos juntos.
En otras palabras: el cuadrado de la hipotenusa es
igual a la suma de los cuadrados de los catetos:
(cateto 1)² + (cateto 2)² = (hipotenusa)²
|
|
3. EXPLICACIÓN DEL TEMA: APLICACIÓN DE PERÍMETRO Y ÁREA
Antes de explicar unos ejercicios prácticos recordemos el concepto de perímetro y área o también en el siguiente vídeo. Ahora sí veamos los
siguientes ejemplos:
A. Vamos a calcular el perímetro y
el área de un triángulo, cuando se conocen 2 lados:
1. Perímetro: Se
conocen sólo dos lados.
Para calcular el tercero, aplicamos el Teorema de
Pitágoras:
(cateto1)² +(cateto2)²
=(hipotenusa)²
(24 dm)² + (20 dm)² = (a)²
576 dm² + 400 dm² = a²
976 dm² = a², entonces, a=31,24 dm
Luego:
P = 24dm + 20dm + 31,24dm = 75,24 dm
|
2. Área:
A = base x altura
2
A = (24 dm)(20 dm)
2
A = 480 dm²
2
A = 240 dm²
|
B. Problemas de aplicación:
1.. Luisa va a remodelar el
piso de la sala
de su apartamento (ver
gráfica). ¿Cuán-
to cuestan los materiales? Si
se sabe
que cada baldosa cuadrada
de 20cmx20cm vale $1050 y el
metro de
listón de guarda escoba
cuesta $650.
|
2,4m
3m B 4m
4,4m
|
Para
saber la cantidad de baldosas debemos calcular el área y para la cantidad de
listón de guarda escoba el perímetro.
Área:
dividimos
la superficie en dos: A y B.
Área
A=(2,4m)(1m)=2,4m²
Área B=(4,4m)(3m)=13,2m²
Área total: 2,4m² + 13,2
m² =15,6 m²
Área de cada baldosa: primero
pasamos la medida a metros. 20cm=0,2m
Área de cada baldosa:
(0,2m)( 0,2m)=0,4m²
Dividimos el área total de la
sala entre el área de la baldosa:
15,6 m² ÷ 0,4m² = 39
Luego, se necesitan 39
baldosas.
Como cada baldosa cuesta $1050.
En todas las baldosas se gasta $40.950.
Perímetro: P=3m+2m+1m+2,4m+4m+4,4m=16,8m
Se necesitan 16, 8 m de listón.
Como cada metro cuesta $650. En
total se gasta $10.920 en listón
Respuesta: Luisa gasta en total $40.950
+ $10.920 = $51.870
2. Veamos otro problema de aplicación, acerca del papel que senecesita para
forrar una caja de cartón.
4. ACTIVIDADES DE EVALUACIÓN:
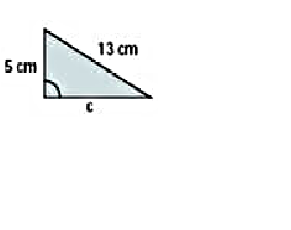
1.Calcule el
área y perímetro de cada figura:
2. ¿Cuánto papel se necesita
para forrar una caja cerrada que mide 35cm de ancho, 55cm de largo y 40cm de
alto?
3. Calcule el perímetro y área de un triángulo que tiene como lados 20m, 15m
y 12m.
4. Calcule el
perímetro y la altura de un triángulo equilatero de lado 12m.
5. Calcule la diagonal de un cuadrado de lado 6cm.
6.
Esteban quiere cercar con alambre un terreno rectangular que mide 120m de
largo y 65m de ancho. ¿Cuántos metros de alambre necesita?
7.
Un granjero le regala un terreno a su hijo y le da las siguientes
instrucciones: Coja este rollo de 150m de alambre y cerque todo el terreno que
pueda, pero debe ser rectangular y uno de sus lados debe dar contra mi parcela
(no necesita cercar ese lado). Haga diferentes esquemas que muestre cómo puede
tomar su herencia el hijo y ¿cuál es la mejor opción para el hijo?
|
una habitación cuadrada de 3m
de lado. La habitación
tiene una ventana de 1m x 1m.
La puerta es de 70cm de ancho
y llega hasta 20cm abajo
del techo. El alto de todas
las paredes es 1,90m. ¿Cuánto
papel decorativo se necesita?
|
|
|
de longitud, en una de las esquinas de un para-
do rectangular de 20m x 30m. Calcular la superficie
del prado en que puede pastar la vaca y la superficie
del prado dónde no puede.
|
|
10..Se construye una pista de patinaje cuadrada sobre
del terreno se siembra de césped. Además, alrededor
del terreno circular se hace una pista de atletismo.
Calcular: A. La superficie total
del terreno. B. La superfi-
cie de la pista de patinaje. C. la superficie que quedó
con césped. D.
Cuántos metros recorre un atleta que le
da una vuelta a la pista de atletismo. E. Si una patinado-
ra da una vuelta alrededor de la pista de patina-
je, ¿cuánto recorre?
|
Tomar foto del desarrollo de cada ejercicio y enviarlo al
correo de su profesor de matemáticas. RECUERDE EN ASUNTO ESCRIBIR: CURSO-APELLIDOS-NOMBRES-
#GUÍA. También pueden enviar las evidencias al grupo de whatsapp
del profesor, según lo acordado en cada curso.
BIBLIOGRAFÍA
/ WEBGRAFÍA:
https://teoremadepitagoras.info/problemas-de-aplicacion-del-teorema-de-pitagoras/






Comentarios
Publicar un comentario